Charles Petzold

A reader of the Russian translation of Applications = Code + Markup: A Guide to the Windows Presentation Foundation — not that I knew there was such a thing; contrary to popular opinion, authors are generally not informed when their books get translated into other languages — wrote me about a program in Chapter 2 that used the Math.Atan2 method, and what should happen when both arguments are zero.

I'm a big fan of Math.Atan2 (or atan2 as it's known in C, or ATAN2 in FORTRAN, where it seems to have originated). In my experience, it's the second most valuable tool in interactive graphics programming after the Pythagorean Theorem.

In .NET the two methods Math.Atan and Math.Atan2 both calculate the arctangent function. As you'll recall, the tangent of an angle θ in a right triangle is the ratio of the opposite side divided by the adjacent side, or y divided by x:

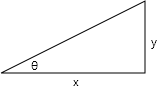
This can be generalized to angles greater than π/2 (90°) or less than zero by representing the angle as a counter-clockwise offset from the positive x axis on a Cartesian plane:

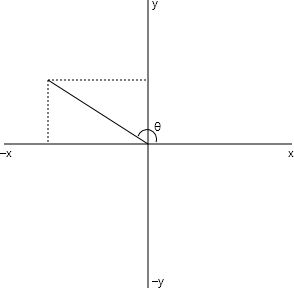
Unlike the sine or cosine functions, the tangent function has singularities. For values of θ equal to π/2 or ‑π/2 (or, in general, nπ/2 for n odd), x equals zero and the tangent goes to either positive or negative infinity, depending on the direction that you approach the angle. (The .NET Math.Tan function returns very large numbers for these values rather than infinity.) The tangent function can be represented like so:

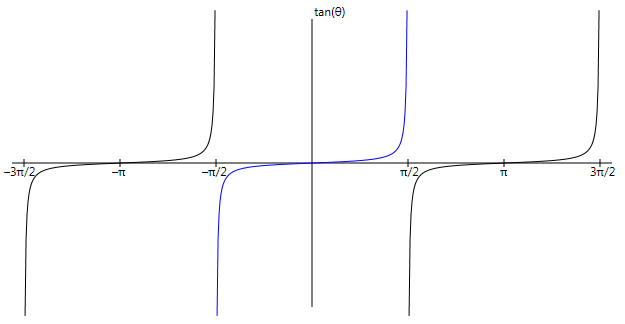
The arctangent is the inverse of that, and the regular Math.Atan method restricts itself to the center of that graph (shown in blue). The method accepts arguments in the range of Double.NegativeInfinity through Double.PositiveInfinity, and returns angles in the range ‑π/2 through π/2, respectively.

The Math.Atan2 method expands the range of the function to –π through π by allowing a second argument:

double angle = Math.Atan2(y, x):

This is a much better inverse of the tangent function. If y and x are the lengths of the opposite and adjacent sides of a right triangle, then the method returns the angle. If (x, y) represents a point on the Cartesian plane, then connecting that point with the origin forms an angle with the positive x axis (as in the second diagram above) and the method returns that angle. This is what makes Math.Atan2 so valuable.

However, a little issue arises when both arguments are zero. Geometrically, a triangle with two sides set to zero is just a point. There is no angle. On the Cartesian plane, the point (x, y) is the origin, so there is no line to form an angle from the positive x axis.

What definitely should not happen is for Math.Atan2 to raise an exception. The IEEE 754 floating-point specification allows signaling in certain circumstances, and this was available in C and C++, but this approach to handling floating point has gone out of favor, and the C# Language Specification (available here) states "The floating-point operators, including the assignment operators, never produce exceptions. Instead, in exceptional situations, floating-point operations produce zero, infinity, or NaN" (§4.1.6).

NaN means "not a number." The IEEE floating-point specification allows special bit configurations that do not correspond to numbers. If you divide a floating-point number by zero, you'll get either positive or negative infinity (also allowed with certain bit configurations). But if you divide a floating-point zero by zero, you get a NaN.

The only method in the .NET Math class that raises exceptions is the integer versions of the Math.Abs for the special case when the argument is MinValue. (For example, Int32.MinValue is the number ‑2,147,483,648, and Math.Abs will raise an OverflowException for that argument because the maximum positive value of an Int32 is 2,147,483,647.) For those floating-point functions that are truly undefined for some values — for example Math.Log with a negative argument — the functions return NaN.

A very good argument could be made that Math.Atan2(0, 0) should return NaN. Indeed, the Wikipedia entry on atan2 indicates that "traditionally, atan2(0,0) is undefined. Some current implementations define it as 0."

An online Fortran 77 Manual says for ATAN2 "It is an error to have both arguments zero." But more recent languages have taken a different approach:

The MSDN documentation for the C function atan2 states "If both parameters of atan2 are 0, the function returns 0."

The MSDN documentation for the .NET Math.Atan2 method states "If y is 0 and x is not negative [which includes 0], θ [the return value] = 0"

The documentation of the Java atan2 method states "If the first argument is positive zero and the second argument is positive, or the first argument is positive and finite and the second argument is positive infinity, then the result is positive zero" which I'm pretty sure applies to both arguments equal to zero.

You'll note that the Java specs refer to "positive zero" because IEEE 754 allows zero to be represented with a sign bit of either 0 or 1. You can create negative zero values in Java with the longBitsToDouble method. In .NET it's a little more difficult but this code creates a double with a value of negative zero:

MemoryStream memStream = new MemoryStream();
BinaryWriter writer = new BinaryWriter(memStream);
writer.Write(Int64.MinValue);
memStream.Seek(0, SeekOrigin.Begin);
BinaryReader reader = new BinaryReader(memStream);
double negativeZero = reader.ReadDouble();

This works because Int64.MinValue (the number ‑9,223,372,036,854,775,808) has a hexadecimal representation of 0x8000000000000000, which is also a double of negative zero. (If you come up with simpler code to create negative zeroes in .NET, I'm curious to see it.)

At any rate, you'll discover that Math.Atan2 returns the following values for combinations of positive zero (the regular zero) and negative zero:

Math.Atan2(0,0) returns 0
Math.Atan2(0,negativeZero) returns π
Math.Atan2(negativeZero,0) returns negativeZero
Math.Atan2(negativeZero,negativeZero) returns ‒π

That third one might be tough to test because if you just use Console.WriteLine to display it, it'll show up as zero. But using the same objects created earlier, try this:

double returnValue = Math.Atan2(negativeZero, 0);
memStream.Seek(0, SeekOrigin.Begin);
writer.Write(returnValue);
memStream.Seek(0, SeekOrigin.Begin);
Console.WriteLine(reader.ReadInt64());

The number displayed will be ‑9,223,372,036,854,775,808, indicating the value returned from Math.Atan2 was truly negative zero.

Of course, most programming languages use the hardware math coprocessor for floating-point. The Intel math coprocessor implements atan2 with the FPATAN instruction, as documented in the Intel Architecture Software Developer’s Manual, Volume 2: Instruction Set Reference , page 3-221. The documentation contains a whole table of various classes of arguments for FPATAN, including negative and positive infinity, with a footnote that explains:

With the FPATAN instruction, the 0/0 or ∞/∞ value is actually not calculated using division. Instead, the arctangent of the two variables is derived from a common mathematical formulation that is generalized to allow complex numbers as arguments. In this complex variable formulation, arctangent(0,0) etc. has well defined values. These values are needed to develop a library to compute transcendental functions with complex arguments, based on the FPU functions that only allow real numbers as arguments.

So there we have it: An actual explanation why atan2 and its cousins return 0 when both arguments are zero. (A rather obscure explanation, of course, but an explanation nevertheless.)